École Internationale Polytechnique de Genève (EIPG) e-Learning platform (LMS & LCMS)
Die Plattform unterstützt 26 Sprachen, sie ist kompatibel mit den SCORM 1.2 und 2004 Standards, und unterstützt verschiedene didaktische Modelle, darunter: Gemischtes, selbstkontrolliertes, kollaboratives und sogar gemeinschaftliches Lernen durch Chat, Wiki, Foren und verschiedene andere Funktionen.
BVMDAE (Lizenzvalidierungsprüfung / Zugang zum Master und zur Promotion)
Sie haben einen Master oder eine Promotion von anderen Institutionen, Sie müssen immer die BVMDAE bestehen.

Unabhängig davon, ob Sie in Oxford, Harvard, Cambridge, Yale, der Open University, UNISA, SAIM, IBS, ICS, Intec, Alison, Coursera oder Fun MOOC studiert haben, müssen Sie die BVMDAE (Bachelor Validation / Master & Doctorate's Access Exam) ablegen. Der BVMDAE wird das zukünftige Instrument zur Bewertung des Bildungsniveaus. Ziel des BVMDAE ist es, das höchstmögliche Niveau zu halten. Bitte beachten Sie, dass Studenten aus Oxford, Harvard, Cambridge und Yale Schwierigkeiten haben, die BVMDAE zu bestehen.
Die EIPG-Online-Berufsbildung (und was ist ...) kann auf postsekundärer, weiterführender und höherer Bildungsebene stattfinden; und kann mit dem Lernsystem interagieren. Auf der postsekundären Ebene wird die berufliche Bildung häufig von hochqualifizierten Fachleuten, technischen Schulen, Community Colleges, britischen Hochschulen, Universitäten, Instituten für Technologie / Polytechnik usw. angeboten.
Bis vor kurzem fand fast die gesamte Berufsausbildung im Klassenzimmer oder am Arbeitsplatz statt, wobei die Schüler von akkreditierten Lehrern oder etablierten Fachleuten berufliche Fähigkeiten und Handelstheorie lernten. Die Online-Berufsausbildung hat jedoch zugenommen und es für Studenten einfacher denn je gemacht, berufliche und allgemeine Fähigkeiten von etablierten Fachleuten in der Branche zu erwerben.
Was ist mit der Anerkennung ... Die BVMDAE (Lizenzvalidierungsprüfung / Zugang zu Master und Promotion) dient als automatisierte Anerkennungsprüfung. Die meisten öffentlichen Universitätsstudenten bestehen diese Prüfung nicht. Nehmen Sie diese Prüfung daher nicht als selbstverständlich an.
Faculty of Management
Doctor Of Science Business Management & Administration or D.Sc. BMA or DBMA
will be of interest to persons wanting to develop skills in Management, Administration, Managerial science and Entrepreneur in general.

Faculty of Medecine
Doctor Of Science Natural Medicine or D.Sc. nMed.
studing anatomy, physiology, biomedical science and medicine in general, as well as any persons wanting to expand their knowledge and understanding of Natural Medicine.

Doctor Of Science Nursing, Nutrition & Naturopathy or D.Sc. nNat.
nursing students will study anatomy, physiology, biomedical science and nursing in general.

Doctor Of Science Psychiatrist & Naturopathy or D.Sc. pNat.
is a physician who specializes in psychiatry, the branch of medicine devoted to the diagnosis, prevention, study, and treatment of mental disorders.

Doctor Of Science Psychology & Naturopathy or D.Sc. sNat.
... attempt to understand the role of mental functions in individual and social behavior, while also exploring the physiological and biological processes that underlie cognitive functions and behaviors.

Doctor Of Science Human Health & Nutrition or D.Sc. HHN
... Human nutrition deals with the provision of essential nutrients in food that are necessary to support human life and health. Poor nutrition is a chronic problem often linked to poverty, food security or a poor understanding of nutrition and dietary practices. Malnutrition and its consequences are large contributors to deaths and disabilities worldwide. Good nutrition is necessary for children to grow physically, and for normal human biological development.

Doctor of Science Biotechnology or D.Sc. BTECH
BioTech or BTCH, also referred to as Biotechnology, is a broad area of biology, involving the use of living systems and organisms to develop or make products. Depending on the tools and applications, it often overlaps with related scientific fields. In the late 20th and early 21st centuries, biotechnology has expanded to include new and diverse sciences, such as genomics, recombinant gene techniques, applied immunology, and development of pharmaceutical therapies and diagnostic tests. The term biotechnology was first used by Karl Ereky in 1919, meaning the production of products from raw materials with the aid of living organisms.

Doctor of Science Biomedical Engineering or D.Sc. BME
Biological medical engineering or bioengineering, BioMed or BME, is the application of principles of biology and the tools of engineering to create usable, tangible, economically-viable products. Biological engineering employs knowledge and expertise from a number of pure and applied sciences, such as mass and heat transfer, kinetics, biocatalysts, biomechanics, bioinformatics, separation and purification processes, bioreactor design, surface science, fluid mechanics, thermodynamics, and polymer science. It is used in the design of medical devices, diagnostic equipment, biocompatible materials, renewable energy, ecological engineering, agricultural engineering, process engineering and catalysis, and other areas that improve the living standards of societies.

Faculty of Science
Doctor of Science Astronomy & Space Science (AS) D.Sc. AS
is the scientific study of celestial objects (such as stars, planets, comets, and galaxies) and phenomena that originate outside the Earth's atmosphere (such as the cosmic background radiation).

EIPG Orbiter II - micro-satellite
Our micro-satellite(Illustrations) with Gyroscope, Geiger Counter, Thermostat and other Scientific Instrument for Pressure / Vacuum Measurement, Electromagnetism, Gas Composition etc. Fully Designed and Developed by Prof. Horstmann and his team of researchers. Cost per unit launched into space 12 000.00€
Doctor of Science Chemistry (CY) D.Sc. CY
is the scientific discipline involved with elements and compounds composed of atoms, molecules and ions: their composition, structure, properties, behavior and the changes they undergo during a reaction with other substances.

Doctor of Science Ecology & Evolution or D.Sc. EYE
Ecology is the scientific analysis and study of interactions among organisms and their environment. Evolution is change in the heritable characteristics of biological populations over successive generations. These characteristics are the expressions of genes that are passed on from parent to offspring during reproduction. Different characteristics tend to exist within any given population as a result of mutation, genetic recombination and other sources of genetic variation.

Doctor of Science Environmental Science & Engineering or D.Sc. ESE
Environmental science is an interdisciplinary academic field that integrates physical, biological and information sciences (including ecology, biology, physics, chemistry, plant science, zoology, mineralogy, oceanography, limnology, soil science, geology and physical geography (geodesy), and atmospheric science) to the study of the environment, and the solution of environmental problems.
Environmental engineering is a professional engineering discipline that encompasses broad scientific topics like chemistry, biology, ecology, geology, hydraulics, hydrology, microbiology, and mathematics to create solutions that will protect and also improve the health of living organisms and improve the quality of the environment. Environmental engineering is a sub-discipline of civil engineering and chemical engineering.

Doctor of Science General Science (GS) D.Sc. GS
... is science in it's basic and pure form. The science which deals with the things related to our life. It includes Biology, chemistry, physics, mathematics and environmental science.

Doctor of Science Humanity & Social Science (HS) D.Sc. HS
... are the study of human behaviour and interaction in social, cultural, environmental, economic and political contexts.

Doctor of Science Life Sciences (LS) D.Sc. LS
the life sciences or biological sciences comprise the branches of science that involve the scientific study of life and organisms – such as microorganisms, plants, and animals including human beings.

Doctor of Science Materials Science (MS) D.Sc. MS
... an interdisciplinary field involving the properties of matter and its applications to various areas of science and engineering. It includes elements of physics and chemistry, as well as chemical, mechanical, civil and electrical engineering.

Doctor of Science Mathematics (MA) D.Sc. MA
from Greek μάθημα máthēma, "knowledge, study, learning", includes the study of such topics as quantity (number theory), structure (algebra), space (geometry), and change (mathematical analysis). It has no generally accepted definition.

Doctor of Science Physics (PH) D.Sc. PH
is the natural science that studies matter, its motion and behavior through space and time, and that studies the related entities of energy and force.
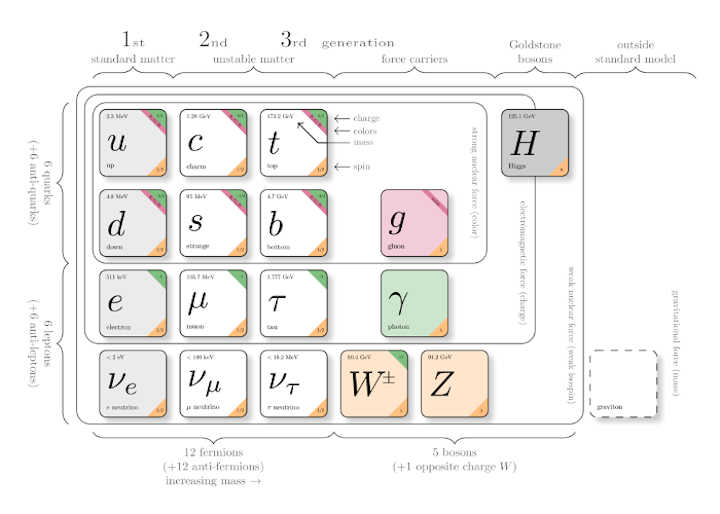
Doctor of Science Statistics (ST) D.Sc. ST
... data collection, organization, analysis, interpretation and presentation. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied.

Faculty of Engineering
Doctor of Science Aerospace Engineering (AE) D.Sc. AE
is the primary field of engineering concerned with the development of aircraft and spacecraft. It has two major and overlapping branches: aeronautical engineering and astronautical engineering.
Water fueled jet Engine
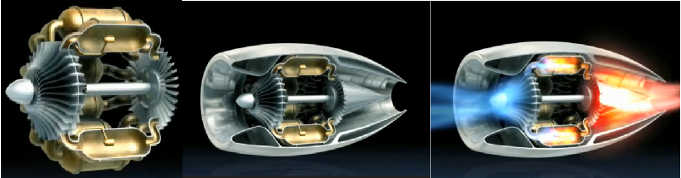
Liquid rocket motors

Doctor of Science Avionics Engineering (AVE) D.Sc. AVE
avionics engineers design and develop aircraft and spacecraft avionic instrumentation. They also conduct research to address problems associated with flight safety systems, landing gear and electronic navigation systems.

Doctor of Science Agricultural Engineering (AG) D.Sc. AG
is the area of engineering concerned with the design, construction and improvement of farming equipment and machinery. Agricultural engineers integrate technology with farming.

Doctor of Science Civil Engineering (CE) D.Sc. CE
is a professional engineering discipline that deals with the design, construction, and maintenance of the physical and naturally built ...

Doctor of Science Chemical Engineering (CH) D.Sc. CH
engineering is a branch of engineering that uses principles of chemistry, physics, mathematics, biology, and economics to efficiently use, produce, design, transport and transform energy and materials.

Doctor of Science Control & Instrumentation Engineering (CI) D.Sc. CI
Instrumentation is defined as the art and science of measurement and control of the process variables within a production or manufacturing area.

Doctor of Science Design Engineering (DE) D.Sc. DE
is a person who may be involved in any of various engineering disciplines including civil, mechanical, electrical, chemical, textiles, aerospace, nuclear, manufacturing, systems, and structural building/architectural.

Doctor of Science Electronics and Communication Engineering (EC) D.Sc. EC
is the application of science and mathematics to practical problems in the field of electronics and communications. Electronics and communications engineers engage in research, design, development and testing of the electronic equipment used in various systems.
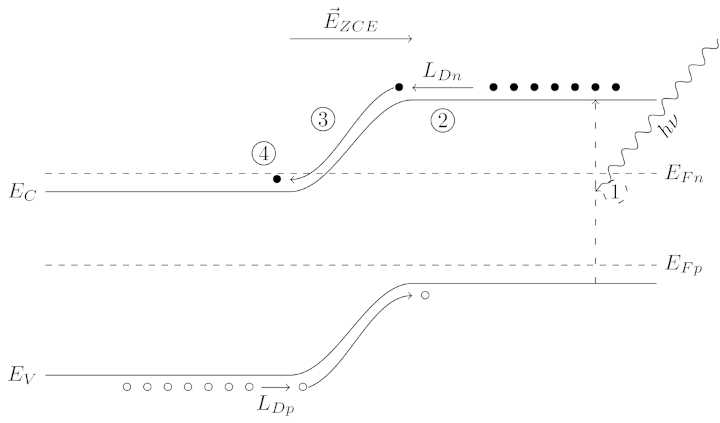
Doctor of Science Electrical & Computer Engineering (EE) D.Sc. EE
... apply electrical, electronic and magnetic theory to obtain solutions for problems related to the development, design and operation of electrical hardware and software, control systems, electrical machines and communications systems.

Doctor of Science Engineering Sciences (ES) D.Sc. ES
is the application of scientific, economic, social, and practical knowledge in order to design, build, and maintain structures, machines, devices, systems, materials and processes.

Doctor of Science Geology and Geophysics Engineering (GE) D.Sc. GE
is the study of geologic structures such as faults and folds. Tectonics deals with large scale Earth structures such as tectonic plates and its deep interior. Geophysics is the study of the Earth by quantitative physical methods. It is an applied science and includes the Earth’s interior, crust, oceans, atmosphere and magnetosphere.

Doctor of Science Information Systems Engineer (IE) D.Sc. IE
design, implement, and maintain computer systems that collect, process, store, and present data.

Doctor of Science Mechanical Engineering (ME) D.Sc. ME
is the discipline that applies engineering, physics, engineering mathematics, and materials science principles to design, analyze, manufacture, and maintain mechanical systems.
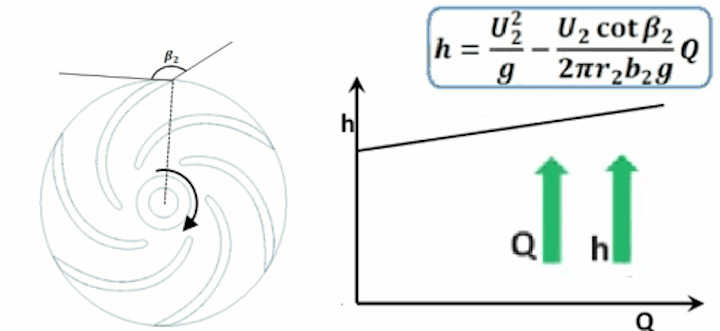
Doctor of Science Mining Engineering (MN) D.Sc. MN
is an engineering discipline that applies science and technology to the extraction of minerals from the earth.

Doctor of Science Materials & Metallurgical Engineering D.Sc. MME
is the study of metals. Combining theory and practice, degree programs cover the mining, extraction, design and processing of metals, as well as how metals react to environmental changes or stress.

Doctor of Science Metallurgical Engineering (MT) D.Sc. MT
is the study of metals. Combining theory and practice, degree programs cover the mining, extraction, design and processing of metals, as well as how metals react to environmental changes or stress.

Doctor of Science Ocean & Atmospheric Engineering (OE) D.Sc. OE
... It includes the study of physical processes acting across the ocean boundaries at the sea floor, coast, and sea surface, and of the ocean's role in the Earth's climate system.

Doctor of Science Petroleum Engineering (PE) D.Sc. PE
is a field of engineering concerned with the activities related to the production of hydrocarbons, which can be either crude oil or natural gas.
Doctor of Science Production and Industrial Engineering (PI) D.Sc. PI
is an interdisciplinary engineering discipline that includes manufacturing technology, engineering sciences, management science, and optimization of complex processes, systems, or organizations.

Doctor of Science Textile Engineering and Fibre Science (TF) D.Sc. TF
the application of scientific and engineering principles to the design and control of all aspects of fiber, textile, and processes, products, and machinery. ... A textile engineer therefore works with textile materials: fibers, yarns, fabrics, and finishes.

Doctor of Science Vehicle Engineer (VE) D.Sc. VE
is the design, manufacture and operation of motorcycles, automobiles and trucks and their respective engineering subsystems.

Faculty of Arts
Doctor of Science Architecture & Planning (AR) D.Sc. AR
is a design and planning for a building, and can contain architectural drawings, specifications of the design, calculations, time planning of the building process, and other documentation.

Doctor of Science Archaeology & Anthropology (AA) D.Sc. AA
archaeology focuses on the study of past human cultures through research of historical sites and artifacts, such as tools, skeletal remains and structural ruins in general.

Faculty of Theology
Doctor of Science Theology (TH) D.Sc. TH
is the study of religion. ... While some students take theology in preparation for a career in the church, you don't have to be religious to have an interest in religion.

Private School - IS Of Jerusalem
From Kindergarten to 12 Grade - Homeschool for Isolated individuals
Diploma of Science High School or Dip.Sc. Hs.
High school graduation is a rite of passage in modern society. Whether you want to impress your friends, get the job of your dreams or qualify for an upcoming promotion, we can help. IS Of Jerusalem has partnered with EIPG Online Academy to complete your primary education with a Diploma. Avoid the stigma attached to GEDs with a diploma that says "I finished High School."
IS Of Jerusalem

EIPG for "IS Of Jerusalem" - High school students raising hands, in classroom with professor
General Information ...
Magnesium aluminate, Synthetic spinel, accidentally produced in the mid-18th century, has been more recently described in scientific publications in 2000 and 2004. By 2015, transparent spinel was made into sheets and other forms by sintering. Synthetic spinel, which looks like glass but has a significantly higher resistance to pressure, can also have applications for military and commercial purposes.

At EIPG our Students produce different Turbo Machines Transparent like Glass, Light as Feathers and Hard as Tanks from Spinel(Magnesium aluminate) formula MgAl2O4.
We are at the point of realizing a 3D Printer for Simply Printing Pumps and PD Pumps(Positive Displacement Pumps) in Spinel at 650°C.
Periodic Table of Chemical Elements
Periodic Table of Chemical Elements for EIPG students


Graphs on all pages are now functional thanks to Prof. Horstmann's Graph API integration
Beautiful Graphs in all browsers
Math Equations on all pages are now functional thanks to Prof. Horstmann's Math API integration
Beautiful Math Equations in all browsers
Integral Formula
\begin{align} f(a) = \frac{1}{2\pi i} \oint_{\gamma}\frac{f(z)}{z-a}dz \end{align}
Dynamic Equations - step by step
Expand the following: \begin{align} (x 1)^2 &= \cssId{Step1}{(x 1)(x 1)} \\[3px] &\cssId{Step2}{{} = x(x 1) 1(x 1)} \\[3px] &\cssId{Step3}{{} = (x^2 x) (x 1)} \\[3px] &\cssId{Step4}{{} = x^2 (x x) 1} \\[3px] &\cssId{Step5}{{} = x^2 2x 1} \end{align}
The Quadratic Formula
When \(a \ne 0\), there are two solutions to \(ax^2 bx c = 0\) and they are
\begin{align} x = {-b \pm \sqrt{b^2-4ac} \over 2a}. \end{align}
Double angle formula for Cosines
\begin{align} \cos(θ φ)=\cos(θ)\cos(φ)−\sin(θ)\sin(φ) \end{align}
Gauss' Divergence Theorem
\begin{align} \int_D ({\nabla\cdot} F)dV=\int_{\partial D} F\cdot ndS \end{align}
Curl of a Vector Field
\begin{align} \vec{\nabla} \times \vec{F} = \left( \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z} \right) \mathbf{i} \left( \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x} \right) \mathbf{j} \left( \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \right) \mathbf{k} \end{align}
Standard Deviation
\begin{align} \sigma = \sqrt{ \frac{1}{N} \sum_{i=1}^N (x_i -\mu)^2} \end{align}
Definition of Christoffel Symbols
\begin{align} (\nabla_X Y)^k = X^i (\nabla_i Y)^k = X^i \left( \frac{\partial Y^k}{\partial x^i} \Gamma_{im}^k Y^m \right) \end{align}
The Lorenz Equations
\begin{align} \dot{x} & = \sigma(y-x) \\ \dot{y} & = \rho x - y - xz \\ \dot{z} & = -\beta z xy \end{align}
Cauchy's Integral Formula
\begin{align} f(a) = \frac{1}{2\pi i} \oint\frac{f(z)}{z-a}dz \end{align}
The Cauchy-Schwarz Inequality
\[ \left( \sum_{k=1}^n a_k b_k \right)^{\!\!2} \leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right) \]
A Cross Product Formula
\[ \mathbf{V}_1 \times \mathbf{V}_2 = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial X}{\partial u} & \frac{\partial Y}{\partial u} & 0 \\ \frac{\partial X}{\partial v} & \frac{\partial Y}{\partial v} & 0 \\ \end{vmatrix} \]
The probability of getting \(k\) heads when flipping \(n\) coins is:
\[P(E) = {n \choose k} p^k (1-p)^{ n-k} \]
An Identity of Ramanujan
\[ \frac{1}{(\sqrt{\phi \sqrt{5}}-\phi) e^{\frac25 \pi}} = 1 \frac{e^{-2\pi}} {1 \frac{e^{-4\pi}} {1 \frac{e^{-6\pi}} {1 \frac{e^{-8\pi}} {1 \ldots} } } } \]
A Rogers-Ramanujan Identity
\[ 1 \frac{q^2}{(1-q)} \frac{q^6}{(1-q)(1-q^2)} \cdots = \prod_{j=0}^{\infty}\frac{1}{(1-q^{5j 2})(1-q^{5j 3})}, \quad\quad \text{for $|q|<1$}. \]
Maxwell's Equations
\begin{align} \nabla \times \vec{\mathbf{B}} -\, \frac1c\, \frac{\partial\vec{\mathbf{E}}}{\partial t} & = \frac{4\pi}{c}\vec{\mathbf{j}} \\ \nabla \cdot \vec{\mathbf{E}} & = 4 \pi \rho \\ \nabla \times \vec{\mathbf{E}}\, \, \frac1c\, \frac{\partial\vec{\mathbf{B}}}{\partial t} & = \vec{\mathbf{0}} \\ \nabla \cdot \vec{\mathbf{B}} & = 0 \end{align}
In-line Mathematics
Finally, while display equations look good for a page of samples, the ability to mix math and text in a paragraph is also important. This expression \(\sqrt{3x-1} (1 x)^2\) is an example of an inline equation. As you see, equations can be used this way as well, without unduly disturbing the spacing between lines.
Trig Identity Formulas
Use these fundemental formulas of trigonometry to help solve problems by re-writing expressions in another equivalent form.
Basic Identities
\[\sin(x)=\frac{1}{\csc(x)}\]
\[\cos(x)=\frac{1}{\sec(x)}\]
\[\tan(x)=\frac{1}{\cot(x)}\]
\[\sec(x)=\frac{1}{\cos(x)}\]
\[\csc(x)=\frac{1}{\sin(x)}\]
\[\cot(x)=\frac{1}{\tan(x)}\]
\[\tan(x)=\frac{\sin(x)}{\cos(x)}\]
\[\sin(-x)=-\sin(x)\]
\[\cos(-x)=\cos(x)\]
\[\tan(-x)=-\tan(x)\]
Pythagorean Identities
\[\sin^2(x) \cos^2(x)=1\]
\[1 \tan^2(x)=\sec^2(x)\]
\[1 \cot^2(x)=\csc^2(x)\]
Sum and Difference Formulas
\[\sin(a b)=\sin(a)\cos(b) \cos(a)\sin(b)\]
\[\sin(a-b)=\sin(a)\cos(b)-\cos(a)\sin(b)\]
\[\cos(a b)=\cos(a)\cos(b)-\sin(a)\sin(b)\]
\[\cos(a-b)=\cos(a)\cos(b) \sin(a)\sin(b)\]
\[\tan(a b)=\frac{\tan(a) \tan(b)}{1-\tan(a)\tan(b)}\]
\[\tan(a-b)=\frac{\tan(a)-\tan(b)}{1 \tan(a)\tan(b)}\]
\[\sin(x) \sin(y)=2\sin(\frac{x y}{2})\cos(\frac{x-y}{2})\]
\[\sin(x)-\sin(y)=2\cos(\frac{x y}{2})\sin(\frac{x-y}{2})\]
\[\cos(x) \cos(y)=2\cos(\frac{x y}{2})\cos(\frac{x-y}{2})\]
\[\cos(x)-\cos(y)=-2\sin(\frac{x y}{2})\sin(\frac{x-y}{2})\]
Double Angle Formulas
\[\sin(2x)=2\sin(x)\cos(x)\]
\[\cos(2x)=\cos^2(x)-\sin^2(x)=1-2\sin^2(x) = 2\cos^2(x)-1\]
Half Angle Formulas
\[\sin(\frac{x}{2})=\pm\sqrt{\frac{1-\cos(x)}{2}}\]
\[\cos(\frac{x}{2})=\pm\sqrt{\frac{1 \cos(x)}{2}}\]
\[\tan(\frac{x}{2})=\pm\sqrt{\frac{1-\cos(x)}{1 \cos(x)}}=\frac{1-\cos(x)}{\sin(x)}=\frac{\sin(x)}{1 \cos(x)}\]
Trigonometric Products
\[\sin(x)\cos(y)=\frac{\sin(x y) \sin(x-y)}{2}\]
\[\cos(x)\cos(y)=\frac{\cos(x y) \cos(x-y)}{2}\]
\[\sin(x)\sin(y)=\frac{\cos(x-y)-\cos(x y)}{2}\]
Chemical Equations on all pages are now functional thanks to Prof. Horstmann's Chemical API integration
Beautiful Chemical Equations in all browsers
$$\ce{Zn^2 <=>[ 2OH-][ 2H ] $\underset{\text{amphoteres Hydroxid}}{\ce{Zn(OH)2 v}}$$ <=>[ 2OH-][ 2H ] $\underset{\text{Hydroxozikat}}{\ce{[Zn(OH)4]^2-}}$$}$$ Organic chemistry molecule ...
$$\ce{CH3\bond{1}} {\stackrel{ \;\;\;\large\ce{CH3} }{\stackrel{|}{\underset{\underset{\huge\ce{Cl}}{|}}{\ce{C}}}}}\ce{-CH3}$$
Chemical Equations (ce) ...
$$\ce{CO2 C -> 2 CO}$$
$$\ce{Hg^2 ->[I-] HgI2 ->[I-] [Hg^{II}I4]^2-}$$
$$C_p[\ce{H2O(l)}] = \pu{75.3 J // mol K}$$
Chemical Formulae
$$\ce{H2O}$$ $$\ce{Sb2O3}$$
Charges
$$\ce{H }$$ $$\ce{CrO4^2-}$$ $$\ce{[AgCl2]-}$$
$$\ce{Y^99 }$$ $$\ce{Y^{99 }}$$
Stoichiometric Numbers
$$\ce{2 H2O}$$ $$\ce{2H2O}$$ $$\ce{0.5 H2O}$$
$$\ce{1/2 H2O}$$ $$\ce{(1/2) H2O}$$ $$\ce{$n$ H2O}$$
Isotopes
$$\ce{^{227}_{90}Th }$$ $$\ce{^227_90Th }$$ $$\ce{^{0}_{-1}n^{-}}$$ $$\ce{^0_-1n-}$$ $$\ce{H{}^3HO}$$ $$\ce{H^3HO}$$
Reaction Arrows
$$\ce{A -> B}$$ $$\ce{A <- B}$$ $$\ce{A <-> B}$$ $$\ce{A <--> B}$$ $$\ce{A <=> B}$$ $$\ce{A <=>> B}$$ $$\ce{A <<=> B}$$ $$\ce{A ->[H2O] B}$$ $$\ce{A ->[{text above}][{text below}] B}$$ $$\ce{A ->[$x$][$x_i$] B}$$
Parentheses, Brackets, Braces
$$\ce{(NH4)2S}$$ $$\ce{[\{(X2)3\}2]^3 }$$ $$\ce{CH4 2 $\left( \ce{O2 79/21 N2} \right)$}$$
States of Aggregation
$$\ce{H2(aq)}$$ $$\ce{CO3^2-_{(aq)}}$$ $$\ce{NaOH(aq,$\infty$)}$$
Crystal Systems
$$\ce{ZnS($c$)}$$ $$\ce{ZnS(\ca$c$)}$$
Variables like x, n, 2n 1
$$\ce{NO_x}$$ $$\ce{Fe^n }$$ $$\ce{x Na(NH4)HPO4 ->[\Delta] (NaPO3)_x x NH3 ^ x H2O}$$
Greek Characters
$$\ce{\mu-Cl}$$ $$\ce{[Pt(\eta^2-C2H4)Cl3]-}$$ $$\ce{\beta }$$ $$\ce{^40_18Ar \gamma{} \nu_e}$$
(Italic) Math
$$\ce{NaOH(aq,$\infty$)}$$ $$\ce{Fe(CN)_{$\frac{6}{2}$$}}$$ $$\ce{X_{$i$}^{$x$}}$$ $$\ce{X_$i$^$x$}$$
Italic Text
$$\ce{$cis${-}[PtCl2(NH3)2]}$$ $$\ce{CuS($hP12$)}$$
Upright Text, Escape Parsing
$$\ce{{Gluconic Acid} H2O2}$$ $$\ce{X_{{red}}}$$ $$\ce{{( )}_589{-}[Co(en)3]Cl3}$$
Bonds
$$\ce{C6H5-CHO}$$ $$\ce{A-B=C#D}$$ $$\ce{A\bond{-}B\bond{=}C\bond{#}D}$$ $$\ce{A\bond{1}B\bond{2}C\bond{3}D}$$ $$\ce{A\bond{~}B\bond{~-}C}$$ $$\ce{A\bond{~--}B\bond{~=}C\bond{-~-}D}$$ $$\ce{A\bond{...}B\bond{....}C}$$ $$\ce{A\bond{->}B\bond{<-}C}$$
Addition Compounds
$$\ce{KCr(SO4)2*12H2O}$$ $$\ce{KCr(SO4)2.12H2O}$$ $$\ce{KCr(SO4)2 * 12 H2O}$$
Oxidation States
$$\ce{Fe^{II}Fe^{III}2O4}$$
Unpaired Electrons, Radical Dots
$$\ce{OCO^{.-}}$$ $$\ce{NO^{(2.)-}}$$
Kröger-Vink Notation
$$\ce{Li^x_{Li,1-2x}Mg^._{Li,x}$$V'_{Li,x}Cl^x_{Cl}}$$ $$\ce{O''_{i,x}}$$ $$\ce{M^{..}_i}$$ $$\ce{$V$^{4'}_{Ti}}$$ $$\ce{V_{V,1}C_{C,0.8}$$V_{C,0.2}}$$
Equation Operators
$$\ce{A B}$$ $$\ce{A - B}$$ $$\ce{A = B}$$ $$\ce{A \pm B}$$
Precipitate and Gas
$$\ce{SO4^2- Ba^2 -> BaSO4 v}$$ $$\ce{A v B (v) -> B ^ B (^)}$$
Other Symbols and Shortcuts
$$\ce{NO^*}$$ $$\ce{1s^2-N}$$ $$\ce{n-Pr}$$ $$\ce{iPr}$$ $$\ce{\ca Fe}$$ $$\ce{A, B, C; F}$$ $$\ce{{and others}}$$
Complex Examples
$$\ce{Zn^2 <=>[ 2OH-][ 2H ] $\underset{\text{amphoteres Hydroxid}}{\ce{Zn(OH)2 v}}$$ <=>[ 2OH-][ 2H ] $\underset{\text{Hydroxozikat}}{\ce{[Zn(OH)4]^2-}}$$}$$ $$K = \frac{[\ce{Hg^2 }][\ce{Hg}]}{[\ce{Hg2^2 }]}$$ $$K = \ce{\frac{[Hg^2 ][Hg]}{[Hg2^2 ]}}$$ $$\ce{Hg^2 ->[I-] $\underset{\mathrm{red}}{\ce{HgI2}}$$ ->[I-] $\underset{\mathrm{red}}{\ce{[Hg^{II}I4]^2-}}$$}$$
Physical Units (pu)
$$\pu{123 kJ}$$ $$\pu{123 mm2}$$ $$\pu{123 J s}$$ $$\pu{123 J*s}$$ $$\pu{123 kJ/mol}$$ $$\pu{123 kJ//mol}$$ $$\pu{123 kJ mol-1}$$ $$\pu{123 kJ*mol-1}$$ $$\pu{1.2e3 kJ}$$ $$\pu{1,2e3 kJ}$$ $$\pu{1.2E3 kJ}$$ $$\pu{1,2E3 kJ}$$
Crystal Systems
$$\ce{ZnS($c$)}$$ $$\ce{ZnS(\ca$c$)}$$
In-line Chemical Equations
Finally, while display equations look good for a page of samples, the ability to mix Chemical Equations and text in a paragraph is also important. This expression \(\ce{Zn^2 <=>[ 2OH-][ 2H ] $\underset{\text{amphoteres Hydroxid}}{\ce{Zn(OH)2 v}}$$ <=>[ 2OH-][ 2H ] $\underset{\text{Hydroxozikat}}{\ce{[Zn(OH)4]^2-}}$$}\) is an example of an inline equation. As you see, equations can be used this way as well, without unduly disturbing the spacing between lines.
